Problem H: 大数因式分解 Pollard_rho 算法详解
[Creator : ]
Description
在线大数分解工具:
https://zh.numberempire.com/numberfactorizer.php
给你一个大数n,将它分解它的质因子的乘积的形式。
首先需要了解Miller_rabin判断一个数是否是素数
大数分解最简单的思想也是试除法,这里就不再展示代码了,就是从2到sqrt(n),一个一个的试验,直到除到1或者循环完,最后判断一下是否已经除到1了即可。
但是这样的做的复杂度是相当高的。一种很妙的思路是找到一个因子(不一定是质因子),然后再一路分解下去。这就是基于Miller_rabin的大数分解法Pollard_rho大数分解。
Pollard_rho算法的大致流程是 先判断当前数是否是素数(Miller_rabin)了,如果是则直接返回。如果不是素数的话,试图找到当前数的一个因子(可以不是质因子)。然后递归对该因子和约去这个因子的另一个因子进行分解。
那么自然的疑问就是,怎么找到当前数n的一个因子?当然不是一个一个慢慢试验,而是一种神奇的想法。其实这个找因子的过程我理解的不是非常透彻,感觉还是有一点儿试的意味,但不是盲目的枚举,而是一种随机化算法。我们假设要找的因子为p,他是随机取一个x1,由x1构造x2,使得{p可以整除x1-x2 && x1-x2不能整除n}则p=gcd(x1-x2,n),结果可能是1也可能不是1。如果不是1就找寻成功了一个因子,返回因子;如果是1就寻找失败,那么我们就要不断调整x2,具体的办法通常是x2=x2*x2+c(c是自己定的)直到出现x2出现了循环==x1了表示x1选取失败重新选取x1重复上述过程。(似乎还存在一个每次找寻范围*2的优化,但是不太懂。。。)
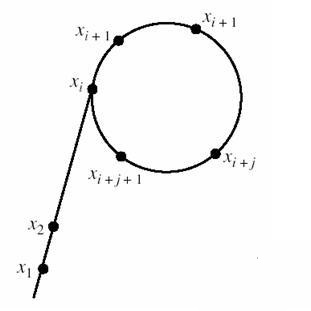
因为x1和x2再调整时最终一定会出现循环,形成一个类似希腊字母rho的形状,故因此得名。
另外通过find函数来分解素数,如果找到了一个素数因子则加入到因子map中,否则如果用Pollard找到一个因子则递归去找素数因子。
https://zh.numberempire.com/numberfactorizer.php
给你一个大数n,将它分解它的质因子的乘积的形式。
首先需要了解Miller_rabin判断一个数是否是素数
大数分解最简单的思想也是试除法,这里就不再展示代码了,就是从2到sqrt(n),一个一个的试验,直到除到1或者循环完,最后判断一下是否已经除到1了即可。
但是这样的做的复杂度是相当高的。一种很妙的思路是找到一个因子(不一定是质因子),然后再一路分解下去。这就是基于Miller_rabin的大数分解法Pollard_rho大数分解。
Pollard_rho算法的大致流程是 先判断当前数是否是素数(Miller_rabin)了,如果是则直接返回。如果不是素数的话,试图找到当前数的一个因子(可以不是质因子)。然后递归对该因子和约去这个因子的另一个因子进行分解。
那么自然的疑问就是,怎么找到当前数n的一个因子?当然不是一个一个慢慢试验,而是一种神奇的想法。其实这个找因子的过程我理解的不是非常透彻,感觉还是有一点儿试的意味,但不是盲目的枚举,而是一种随机化算法。我们假设要找的因子为p,他是随机取一个x1,由x1构造x2,使得{p可以整除x1-x2 && x1-x2不能整除n}则p=gcd(x1-x2,n),结果可能是1也可能不是1。如果不是1就找寻成功了一个因子,返回因子;如果是1就寻找失败,那么我们就要不断调整x2,具体的办法通常是x2=x2*x2+c(c是自己定的)直到出现x2出现了循环==x1了表示x1选取失败重新选取x1重复上述过程。(似乎还存在一个每次找寻范围*2的优化,但是不太懂。。。)
因为x1和x2再调整时最终一定会出现循环,形成一个类似希腊字母rho的形状,故因此得名。

另外通过find函数来分解素数,如果找到了一个素数因子则加入到因子map中,否则如果用Pollard找到一个因子则递归去找素数因子。
1 #include<iostream> 2 #include<ctime> 3 #include<algorithm> 4 #include<map> 5 using namespace std; 6 typedef long long ll; 7 map<ll, int>m; 8 const int mod = 10000019; 9 const int times = 50;//测试50次 10 ll mul(ll a, ll b, ll m) 11 //求a*b%m 12 { 13 ll ans = 0; 14 a %= m; 15 while(b) 16 { 17 if(b & 1)ans = (ans + a) % m; 18 b /= 2; 19 a = (a + a) % m; 20 } 21 return ans; 22 } 23 ll pow(ll a, ll b, ll m) 24 //a^b % m 25 { 26 ll ans = 1; 27 a %= m; 28 while(b) 29 { 30 if(b & 1)ans = mul(a, ans, m); 31 b /= 2; 32 a = mul(a, a, m); 33 } 34 ans %= m; 35 return ans; 36 } 37 bool Miller_Rabin(ll n, int repeat)//n是测试的大数,repeat是测试重复次数 38 { 39 if(n == 2 || n == 3)return true;//特判 40 if(n % 2 == 0 || n == 1)return false;//偶数和1 41 42 //将n-1分解成2^s*d 43 ll d = n - 1; 44 int s = 0; 45 while(!(d & 1)) ++s, d >>= 1; 46 //srand((unsigned)time(NULL));在最开始调用即可 47 for(int i = 0; i < repeat; i++)//重复repeat次 48 { 49 ll a = rand() % (n - 3) + 2;//取一个随机数,[2,n-1) 50 ll x = pow(a, d, n); 51 ll y = 0; 52 for(int j = 0; j < s; j++) 53 { 54 y = mul(x, x, n); 55 if(y == 1 && x != 1 && x != (n - 1))return false; 56 x = y; 57 } 58 if(y != 1)return false;//费马小定理 59 } 60 return true; 61 } 62 ll gcd(ll a, ll b) 63 { 64 return b == 0 ? a : gcd(b, a % b); 65 } 66 ll pollard_rho(ll n, ll c)//找到n的一个因子 67 { 68 ll x = rand() % (n - 2) + 1; 69 ll y = x, i = 1, k = 2; 70 while(1) 71 { 72 i++; 73 x = (mul(x, x, n) + c) + n;//不断调整x2 74 ll d = gcd(y - x, n); 75 if(1 < d && d < n) 76 return d;//找到因子 77 if(y == x) 78 return n;//找到循环,返回n,重新来 79 if(i == k)//一个优化 80 { 81 y = x; 82 k <<= 1; 83 } 84 } 85 } 86 void Find(ll n, ll c) 87 { 88 if(n == 1)return;//递归出口 89 90 if(Miller_Rabin(n, times))//如果是素数,就加入 91 { 92 m[n]++; 93 return; 94 } 95 96 ll p = n; 97 while(p >= n) 98 p = pollard_rho(p, c--);//不断找因子,知道找到为止,返回n说明没找到 99 100 Find(p, c); 101 Find(n / p, c); 102 } 103 int main() 104 { 105 ll n;srand((unsigned)time(NULL)); 106 while(cin >> n) 107 { 108 m.clear(); 110 Find(n, rand() % (n - 1) + 1);//这是自己设置的一个数 111 cout<<n<<" = "; 112 for(map<ll ,int>::iterator it = m.begin(); it != m.end();) 113 { 114 cout<<it->first<<" ^ "<<it->second; 115 if((++it) != m.end()) 116 cout<<" * "; 117 } 118 cout<<endl; 119 } 120 return 0; 121 }
HINT
from random import randint
def gcd(a,b):
while b!=0:
a,b=b,a%b
return a
def powm(a,b,m):
ret=1
while b:
if b&1:
ret=ret*a%m
b>>=1
a=a*a%m
return ret
def isPrime(n,t=15):
if n<=1: return 0
if n==2: return 1
if not n&1: return 0
t=min(n-2,t)
ret=1
for i in range(t):
a=randint(2,n-1)
if powm(a,n-1,n)!=1:return 0
return 1
def factor(n):
if n<2:return [n]
if isPrime(n):return [n]
fact=1
y=x=c=2 #y=x*x+c
cyc=2
while fact==1:
for i in range(cyc):
y=(y*y+c)%n
if x==y:
c=randint(1,n-1)
continue
if y-x<2:continue
## time.sleep(0.5)
fact=gcd(y-x,n)
if fact>1:break
x=y
cyc*=2
return factor(n//fact)+factor(fact)
def test(a,d=100):
sum=0
for i in range(a,a+d):
if isPrime(i):
print(i)
sum+=1
print("cnt:",sum)
def intLen(x):
ret=1
while x>9:
x//=10
ret+=1
return ret
def showfj(x):
print()
print(x,intLen(x))
oms=time.time()
a=factor(x)
a.sort()
b=list(map(intLen,a))
print(a)
print(b)
print(time.time()-oms)
x= int(input())
a=factor(x)
a.sort()
al=len(a)
for i in range(al):
if i==0: print(a[i],end='')
else:
print("*",end='')
print(a[i],end='')
##test(111111111111,100)
##showfj(111111111149*111111111187)
def gcd(a,b):
while b!=0:
a,b=b,a%b
return a
def powm(a,b,m):
ret=1
while b:
if b&1:
ret=ret*a%m
b>>=1
a=a*a%m
return ret
def isPrime(n,t=15):
if n<=1: return 0
if n==2: return 1
if not n&1: return 0
t=min(n-2,t)
ret=1
for i in range(t):
a=randint(2,n-1)
if powm(a,n-1,n)!=1:return 0
return 1
def factor(n):
if n<2:return [n]
if isPrime(n):return [n]
fact=1
y=x=c=2 #y=x*x+c
cyc=2
while fact==1:
for i in range(cyc):
y=(y*y+c)%n
if x==y:
c=randint(1,n-1)
continue
if y-x<2:continue
## time.sleep(0.5)
fact=gcd(y-x,n)
if fact>1:break
x=y
cyc*=2
return factor(n//fact)+factor(fact)
def test(a,d=100):
sum=0
for i in range(a,a+d):
if isPrime(i):
print(i)
sum+=1
print("cnt:",sum)
def intLen(x):
ret=1
while x>9:
x//=10
ret+=1
return ret
def showfj(x):
print()
print(x,intLen(x))
oms=time.time()
a=factor(x)
a.sort()
b=list(map(intLen,a))
print(a)
print(b)
print(time.time()-oms)
x= int(input())
a=factor(x)
a.sort()
al=len(a)
for i in range(al):
if i==0: print(a[i],end='')
else:
print("*",end='')
print(a[i],end='')
##test(111111111111,100)
##showfj(111111111149*111111111187)
