Problem G: 2018NOIP提高组DAY2第二题 填数游戏(game)
[Creator : ]
Description
小D特别喜欢玩游戏。这一天,他在玩一款填数游戏。
这个填数游戏的棋盘是一个n × m的矩形表格。玩家需要在表格的每个格子中填入一个数字(数字 0 或者数字 1),填数时需要满足一些限制。
下面我们来具体描述这些限制。
为了方便描述,我们先给出一些定义:
• 我们用每个格子的行列坐标来表示一个格子,即(行坐标,列坐标)。(注意:行列坐标均从 0 开始编号)
• 合法路径 P: 一条路径是合法的当且仅当:
1. 这条路径从矩形表格的左上角的格子(0,0)出发,到矩形的右下角格子(n − 1, m − 1)结束;
2. 在这条路径中, 每次只能从当前的格子移动到右边与它相邻的格子, 或者从当前格子移动到下面与它相邻的格子。
例如: 在下面这个矩形中,只有两条路径是合法的,它们分别是p1: (0,0) → (0,1) →(1,1)和p2: (0,0) → (1,0) → (1,1)。
这个填数游戏的棋盘是一个n × m的矩形表格。玩家需要在表格的每个格子中填入一个数字(数字 0 或者数字 1),填数时需要满足一些限制。
下面我们来具体描述这些限制。
为了方便描述,我们先给出一些定义:
• 我们用每个格子的行列坐标来表示一个格子,即(行坐标,列坐标)。(注意:行列坐标均从 0 开始编号)
• 合法路径 P: 一条路径是合法的当且仅当:
1. 这条路径从矩形表格的左上角的格子(0,0)出发,到矩形的右下角格子(n − 1, m − 1)结束;
2. 在这条路径中, 每次只能从当前的格子移动到右边与它相邻的格子, 或者从当前格子移动到下面与它相邻的格子。
例如: 在下面这个矩形中,只有两条路径是合法的,它们分别是p1: (0,0) → (0,1) →(1,1)和p2: (0,0) → (1,0) → (1,1)。
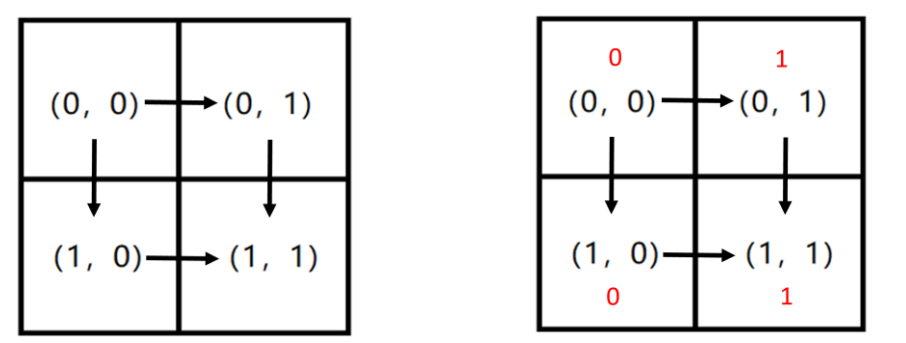
对于一条合法的路径p,我们可以用一个字符串w(p)来表示,该字符串的长度为n+m−2,其中只包含字符“R”或者字符“D”,第i个字符记录了路径P中第i步的移动方法,“R”表示移动到当前格子右边与它相邻的格子,“D”表示移动到当前格子下面与它相邻的格子。例如,上图中对于路径p1,有w(p1)="RD";而对于另一条路径p2,有w(p2)="DR"。
同时, 将每条合法路径p经过的每个格子上填入的数字依次连接后,会得到一个长度为n+m−1的01字符串,记为 s(p)。例如,如果我们在格子(0,0)和(1,0)上填入数字0,在格子(0,1)和(1,1)上填入数字 1(见上图红色数字)。 那么对于路径p1, 我们可以得到s(p1) = "011",对于路径p2,有s(p2) = "001"。
游戏要求小D找到一种填数字0、1的方法,使得对于两条路径p1,p2,如果w(p1)>w(p2),那么必须s(p1) ≤s(p2)。 我们说字符串a比字符串b小,当且仅当字符串a的字典序小于字符串b的字典序,字典序的定义详见第一题。但是仅仅是找一种方法无法满足小D的好奇心,小D更想知道这个游戏有多少种玩法,也就是说,有多少种填数字的方法满足游戏的要求?
小D能力有限,希望你帮助他解决这个问题,即有多少种填 0、1的方法能满足题目要求。由于答案可能很大,你需要输出答案对10^9+7取模的结果。
Input
输入文件共一行,包含两个正整数 n、 m, 由一个空格分隔, 表示矩形的大小。 其中 n 表示矩形表格的行数, m 表示矩形表格的列数。
Output
输出共一行,包含一个正整数,表示有多少种填 0、 1 的方法能满足游戏的要求。
注意: 输出答案对 109+7 取模的结果。
注意: 输出答案对 109+7 取模的结果。
Sample Input Copy
2 2
Sample Output Copy
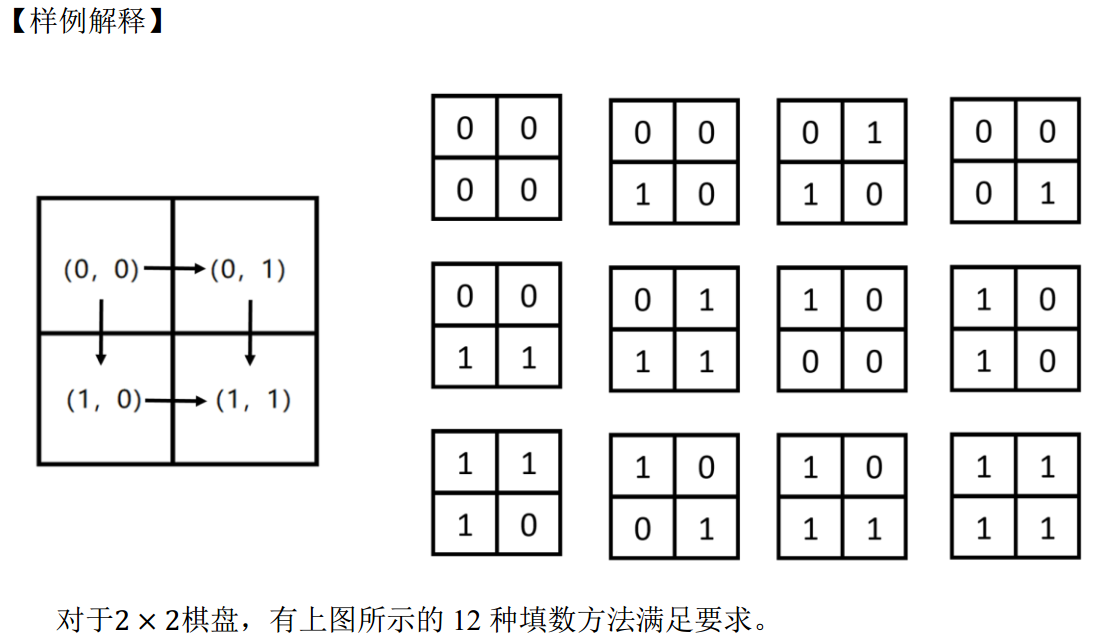
12
HINT
【输入样例2】
3 3
【输出样例2】
112
【输入样例3】
5 5
【输出样例3】
7136