Problem D: NHJM244 LX的能量核心
[Creator : ]
Description
魔王 LX 的能量来源于一个结界,这个结界是一个二维平面,其中有 $n$ 个能量晶体,每个晶体都有自己的坐标,可以看成是平面中的一个点。
小K发现,以 $4$ 个能量晶体作为顶点组成 $1$ 个正方形时,就构成了一个能量核心。如果小K能找到所有能量核心并将之打破,就能削弱魔王 LX 的能力。
给出 $n$ 个能量晶体的坐标,求出有多少个能量核心。
小K发现,以 $4$ 个能量晶体作为顶点组成 $1$ 个正方形时,就构成了一个能量核心。如果小K能找到所有能量核心并将之打破,就能削弱魔王 LX 的能力。
给出 $n$ 个能量晶体的坐标,求出有多少个能量核心。
Input
- 第一行输入一个整数 $n$,代表能量晶体的个数。$(1 \leq n \leq 500)$。
- 接下来 $n$ 行,每行输入两个整数 $x_i, y_i$,代表每个晶体的坐标。$(-50 \leq x_i, y_i \leq 50)$。每个坐标都不会重复。
- 接下来 $n$ 行,每行输入两个整数 $x_i, y_i$,代表每个晶体的坐标。$(-50 \leq x_i, y_i \leq 50)$。每个坐标都不会重复。
Output
- 输出能量核心的个数。
Sample Input Copy
7
0 0
0 1
1 0
1 1
1 2
2 1
2 2
Sample Output Copy
3
HINT
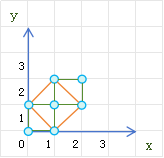
### 样例解释
- 第 $1$ 个正方形的四个顶点:$(0, 0), (0, 1), (1, 0), (1, 1)$
- 第 $2$ 个正方形的四个顶点:$(1, 1), (1, 2), (2, 1), (2, 2)$
- 第 $3$ 个正方形的四个顶点:$(0, 1), (1, 0), (1, 2), (2, 1)$
- 第 $1$ 个正方形的四个顶点:$(0, 0), (0, 1), (1, 0), (1, 1)$
- 第 $2$ 个正方形的四个顶点:$(1, 1), (1, 2), (2, 1), (2, 2)$
- 第 $3$ 个正方形的四个顶点:$(0, 1), (1, 0), (1, 2), (2, 1)$
共找到 $3$ 个能量核心。