1823: 三角形钉子下落(动规课程D)(5)
[Creator : ]
Description
墙上有三角形木板, 上面钉着 n(n+1)/2 颗钉子。 下面有(n+1)个格子, 例如 n=5 时如下图 1:
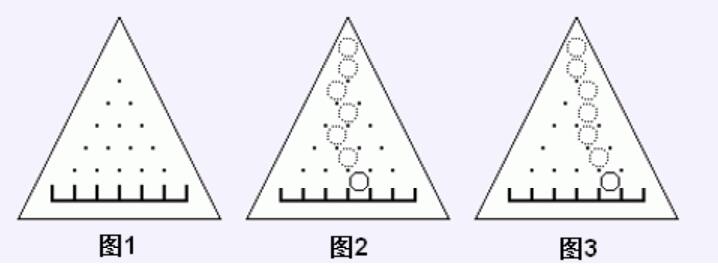
钉子和周围的钉子的距离都是 d。 让一个直径略小于 d 的小球中心正对着上面的钉子在板上自由落体, 小球每碰到一个钉子都可能落向左边或右边。 图 2 就是小球落入第 5 格的一条可能的路径。
现在有些钉子被拔掉(保证第 n 行的钉子都不会拔掉), 小球到被拔掉钉子的位置, 就只能垂直下落。 如图 3, 其中第 4 行的第 2 个钉子被拔掉了。 问小球落入下面每一个格子各有多少可能路径?
Input
第 1 行为整数 n(2<=n<=50)。
以下 n 行依次为木板上从上至下 n 行钉子的信息,每行中 1 表示钉子还在, 0 表示钉子被拔去。
以下 n 行依次为木板上从上至下 n 行钉子的信息,每行中 1 表示钉子还在, 0 表示钉子被拔去。
Output
n+1 个整数。
Sample Input Copy
5
1
1 0
1 1 1
1 0 1 1
1 1 1 1 1
Sample Output Copy
1 2 5 4 2 0